V. V. Chupin, D. E. Chernogubov
STABILITY OF FLEXIBLE SPHERICAL PANELS OF VARIABLE THICKNESS UNDER VARIOUS FIXING CONDITIONS
DOI: 10.17804/2410-9908.2015.5.045-057 An algorithm for studying the stability of elastic thin-shell systems consisting of shells of revolution supported by rings. On the basis of this algorithm, a computer program has been written that allows one to determine the values of critical loads and buckling modes of shells in a wide range of geometrical, physical and power parameters. The stability of spherical panels of variable thickness under different conditions of fixing has been studied
Keywords: shell, stability, critical load References:
- Valishvili N.V. Metody rascheta obolochek vrashcheniya na ETSVM [Methods for Calculating Shells of Revolution on a Computer]. M., Mashinostroenie Publ., 1976, 278 p. (In Russian).
- Volmir A.S. Ustoichivost deformiruemyh sistem [The Stability of Deformable Systems]. M., Nauka Publ., 1976, 984 p. (In Russian).
- Godunov S.K. On the numerical solution of boundary value problems for systems of ordinary differential equations. Uspekhi Matematicheskikh Nauk, 1961, no. 16, pp. 171–174. (In Russian).
- Grigolyuk E.I., Shalashilin V.I. Problemy nelineinogo deformirovaniya [Problems of Nonlinear Deformation]. M., Nauka Publ., 1988, 231 p. (In Russian).
- Grigorenko Ya.M. Izotropnye i anizotropnye sloistye obolochki vrashcheniya peremennoi zhestkosti [Isotropic and Anisotropic Laminated Shells of Revolution of Variable Rigidity]. Kiev, Naukova Dumka Publ., 1973, 228 p. (In Russian).
- Grigorenko Ya.M., Kryukov N.N. Solving nonlinear boundary value problems of the statics of flexible laminated shells in the supercritical region. Soviet Applied Mechanics, 1983, Vol. 19, iss. 3, pp 217–221.
- Emelyanov I.G. Kontaktnye zadachi teorii obolochek [Contact Problems of the Theory of Shells]. Ekaterinburg, UrO RAN, 2009, 184 p. (In Russian).
- Kantorovich L.V., Akilov G.R. Funktsionalnyi analiz v normirovannykh prostranstvakh [Functional Analysis in Normed Spaces]. M., Fizmatgiz Publ., 1959, 684 p. (In Russian).
- Karmishin A.V., Lyaskovets V.A., Myachenkov V.I., Frolov A.N. Statika i dinamika tonkostennykh obolochechnykh konstruktsiy [Statics and Dynamics of Thin-Walled Shell Structures]. M., Mashinostroenie Publ., 1975, 376 p. (In Russian).
- Klimanov V.I., Chupin V.V. Statika i Ustoichivost gibkikh neodnorodnykh obolochechnykh sistem [Statics and Stability of Flexible Shell Heterogeneous Systems]. Krasnoyarsk, KrasGU Publ., 1986, 182 p. (In Russian).
- Korovaitsev A.V. An algorithm for studying the state of shallow shells of revolution under axisymmetric large displacements. Izvestiya vuzov. Mashinostroenie, 1981, iss. 10, pp. 12–15. (In Russian).
- Mushtari Kh.M., Galimov K.Z. Nelineynaya teoriya uprugikh obolochek [The Nonlinear Theory of Elastic Shells]. Kazan, Tatknigoizdat Publ., 1957, 431 p. (In Russian).
- Myachenkov V.I., Grigoriev I.V. Raschet obolochechnykh konstruktsiy na EVM [Calculation of Shell Structures on a Computer]. M., Mashinostroenie Publ., 1981, 216 p. (In Russian).
- Novozhilov V.V. Osnovy nelineynoy teorii uprugosti [Fundamentals of Nonlinear Elasticity]. M., Gostekhizdat Publ., 1948, 211 p. (In Russian).
- Reissner E. Linear and nonlinear theory of shells. In: Tonkostennye obolochechnye konstruktsii [Thin-Walled Shell Structures]. M., Mashinostroenie Publ., 1980, pp. 55–69. (In Russian).
- Chupin V.V., Chernogubov D.E. Stability of elastic composite shell structures under axisymmetric loading. In: Stroitelstvo i obrazovanie [Civil Engineering and Education]. Ekaterinburg, UrFU, 2011, iss. 14, pp. 29–32. (In Russian).
- Shapovalov L.A. Equations of thin elastic shells for asymmetric deformations. Mechanics of Solids, 1976, iss. 3, pp. 62–72.
В. В. Чупин, Д. Е. Черногубов
УСТОЙЧИВОСТЬ ГИБКИХ СФЕРИЧЕСКИХ ПАНЕЛЕЙ ПЕРЕМЕННОЙ ТОЛЩИНЫ ПРИ РАЗЛИЧНЫХ УСЛОВИЯХ ЗАКРЕПЛЕНИЯ
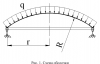
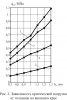
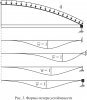
Разработан алгоритм исследования устойчивости упругих тонкостенных оболочечных систем, состоящих из оболочек вращения подкрепленных кольцами. На основе данного алгоритма написана программа для ЭВМ, позволяющая определять величины критических нагрузок и формы потери устойчивости оболочек в широком диапазоне изменения геометрических, физических и силовых параметров. Исследована устойчивость сферических панелей переменной толщины при различных условиях закрепления.
Ключевые слова: : оболочка, устойчивость, критическая нагрузка Библиография:
- Валишвили Н. В. Методы расчета оболочек вращения на ЭЦВМ. – М. : Машиностроение, 1976. – 278 с.
- Вольмир А. С. Устойчивость деформируемых систем. – М. : Наука, 1976. – 984 с.
- Годунов С. К. О численном решении краевых задач для систем обыкновенных линейных дифференциальных уравнений // Успехи математических наук. – 1961. – Т. 16, вып. 3. – С. 171–174.
- Григолюк Э. И., Шалашилин В. И. Проблемы нелинейного деформирования. – М. : Наука, 1988. – 231 с.
- Григоренко Я. М. Изотропные и анизотропные слоистые оболочки вращения переменной жесткости. – Киев : Наукова думка, 1973. – 228 с.
- Grigorenko Ya. M., Kryukov N. N. Solving nonlinear boundary-value problems of the statics of flexible laminated shells in the supercritical region // Soviet Applied Mechanics. – 1983. – Vol. 19, iss. 3. – P. 217–221.
- Емельянов И. Г. Контактные задачи теории оболочек. – Екатеринбург : УрО РАН, 2009. – 184 с.
- Канторович Л. В., Акилов Г. Р. Функциональный анализ в нормированных пространствах. М. : Физматгиз, 1959. – 684 с.
- Статика и динамика тонкостенных оболочечных конструкций / А. В. Кармишин, В. А. Лясковец, В. И. Мяченков, А. Н. Фролов. – М. : Машиностроение, 1975. – 376 с.
- Климанов В. И., Чупин В. В. Статика и устойчивость гибких неоднородных оболочечных систем. – Красноярск : КрасГУ, 1986. – 182 с.
- Коровайцев А. В. Об одном алгоритме исследования состояния непологих оболочек вращения при больших осесимметричных перемещениях // Изв. вузов. Машиностроение. – 1981. – № 10. – С.12–15.
- Муштари Х. М., Галимов К. З. Нелинейная теория упругих оболочек. – Казань : Таткнигоиздат, 1957. – 431 с.
- Мяченков В. И., Григорьев И. В. Расчет оболочечных конструкций на ЭВМ. Справочник. – М. : Машиностроение, 1981. – 216 с.
- Новожилов В. В. Основы нелинейной теории упругости. – М. : Гостехиздат, 1948. – 211 с.
- Рейсснер Е. Линейная и нелинейная теория оболочек // Тонкостенные оболочечные конструкции. – М. : Машиностроение, 1980. – С. 55–69.
- Чупин В. В., Черногубов Д. Е. Устойчивость упругих составных оболочечных конструкций при осесимметричном нагружении // Строительство и образование: сборник научных трудов. – Екатеринбург : УрФУ, 2011. – Вып 14. – С. 29–32.
- Shapovalov L. A. Equations of thin elastic shells for non-symmetric deformations // Mechanics of Solids. – 1976. – Iss. 3 – P. 62–72.
Библиографическая ссылка на статью
Chupin V. V., Chernogubov D. E. Stability of Flexible Spherical Panels of Variable Thickness under Various Fixing Conditions // Diagnostics, Resource and Mechanics of materials and structures. -
2015. - Iss. 5. - P. 45-57. - DOI: 10.17804/2410-9908.2015.5.045-057. -
URL: http://dream-journal.org/issues/2015-5/2015-5_36.html (accessed: 16.04.2025).
|